
Mark Ford and Ali Nadim
Department of Physics
Boston University
There is a general set of problems in fluid dynamics involving migration of droplets and bubbles, having applications in tertiary oil recovery, materials processing in space, and related fields. An example is migration of drops under the influence of gravity and/or thermal gradients, explored here in the context of a numerical simulation. The simulation represents the height profile of a 3-dimensional drop, rolling along a solid plane inclined at 20 degrees to the horizontal. By using the MacCormack Method, the Reynolds flux equation – a non-linear partial differential equation – is integrated over a 500 by 500 node mesh on a Thinking Machines Corporation CM-5. Furthermore, the numerical scheme incorporates the effects of Van der Walls forces, slip, a precursor film and surface tension, besides the customary fluid parameters of viscosity, density and so forth.
Video Sequences

A drop of oil is deposited on a horizontal brass rod, on which a uniform temperature gradient is imposed. The drop exhibits thermocapillary migration, moving away from the hotter side of the rod.

Fine powder is deposited in the drop, tracing pathlines which reveal vigorously active vortices in the migrating drops.

The 3-D Reynolds Lubrication Equation is numerically simulated with the MacCormack scheme on a 500 x 500 node, finite difference mesh, using a CM-5 supercomputer. Gravity and capillary effects are present, slip is equal to zero, and there is precursor film. This simulation represents the transient height of the drop scaled by 100 to create a surface plot. Grey areas represent the precursor film, while shades from blue to red provide additional height and shape information about the droplet. A detailed explanation of details of this sequence appears below.
Still Images
The grey area represents the “plate” on which the simulation took place. The chromatic colors represent height values of the droplet. NAG Explorer was used to do the rendering.
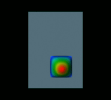
Initially, the drop is cap-shaped, with a square base.
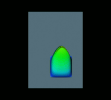
However, as the shape evolves in time, the apex shifts in the direction of inclination.

Here is a front view of the droplet at time step 140 (the viewpoint is elevated)

After 33000 time steps, the drop is characteristically stretched, retaining the square base, yet manifesting a pronounced elongation in the direction of travel. Moreover, a noticeable rim-structure forms. Should the evolution be allowed to continue, one expects the eventual formation of rivulets or a tail.
Hardware: Thinking Machines Corporation CM-5 and Silicon Graphics Onyx at Boston University.
Software: Program written in CM Fortran, 2-D graphics written in C and OpenGL. 3-D graphics in NAG Iris Explorer.
Graphics programming and video production: Kathleen Curry (kat@bu.edu), Scientific Computing and Visualization Group, Boston University.
Acknowledgments: Grateful acknowledgment is made to the American Chemical Society (Petroleum Research Fund) for having funded this research and to Howe Laboratories, NY.
