Rio Yokota, University of Bristol, U.K.
Lorena A. Barba, Boston University
Matthew Knepley, University of Chicago
Many applications in computational science need to approximate a function based on ?nite data. When the data are in a certain sense “scattered” in their domain, one very powerful technique is radial basis function (RBF) interpolation. For many years, the wide applicability of RBF interpolation was hindered by its numerical difficulty and expense. Indeed, in their mathematical expression, RBF methods produce an ill-conditioned linear system, for which a direct solution becomes prohibitive for more than a few thousand data points.
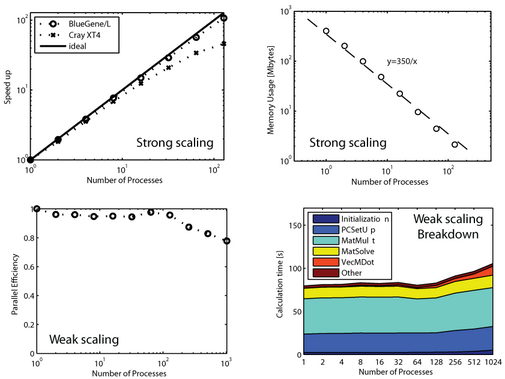
We have developed a parallel algorithm for RBF interpolation that exhibits O(N) complexity, requires O(N) storage, and scales excellently up to a thousand processes. The algorithm uses the GMRES iterative solver with a restricted additive Schwarz method (RASM) as a preconditioner and a fast matrix-vector algorithm. Previous fast RBF methods — achieving at most O(N log N) complexity — were developed using multiquadric and polyharmonic basis functions. In contrast, the present method uses Gaussians with a small variance. The fast decay of the Gaussian basis function allows rapid convergence of the iterative solver even when the subdomains in the RASM are very small. The method was implemented in parallel using the PETSc library (developer version). Numerical experiments demonstrate its capability in problems of RBF interpolation with more than 50 million data points, timing at 106 seconds (19 iterations for an error tolerance of 10e−15) on 1024 processors of a Blue Gene/L (700 MHz PowerPC processors).
The parallel code is freely available in the open-source model. http://code.google.com/p/petrbf/
Radial Basis Function (RBF) Interpolation
Approximate a function by:
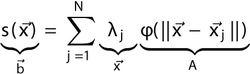
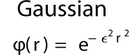
Domain Decomposition Methods
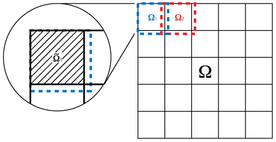
Domain decomposition methods can be used to solve the linear system on highly parallel architectures by distributing the problem.
Mathematically it can be written as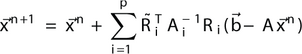 
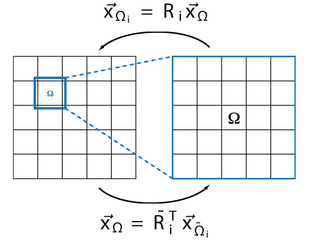
is the restriction operator, which maps the elements onto the overlapping subdomain.
is the projection operator, which maps the elements onto the overlapping subdomain.
Restricted Additive Schwarz Method (RASM)
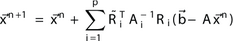
For Gaussian basis functions the RASM serves as a preconditioner and parallelization technique. This particular basis function is a perfect match for the RASM.
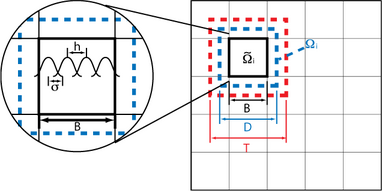
Parameters in RASM
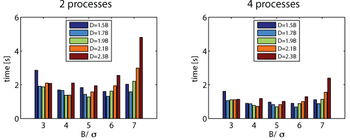
The size of the non-overlapping subdomain B, the overlapping subdomain D, and the domain to be considered in the matrix-vector multiplication T have a large impact on the calculation time. It is the relative size of these domains compared to s that makes the difference. This is independent of the number of elements and the number of processes.
Complexity and Memory Usage
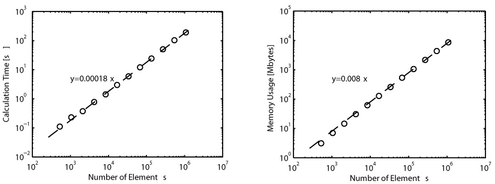
When the number of elements N is increased, the calculation time and memory usage of the present method increases as O(N). This is superior to other RBF interpolation methods which scale as O(N log N)
Parallel Scalability
For the parallel calculations we used the Blue Gene/L machine at Boston University.
