Fast SVM Classification

Huseyin Ozkan (MS ’11)
Dr. Fatih Porikli (Mitsubishi Electric Research Laboratory), Prof. Venkatesh Saligrama, Prof. Janusz Konrad

Funding: Mitsubishi Electric Research Laboratories

Background: Support Vector Machine (SVM) is one of the most popular classification algorithms used in machine learning. It is widely used in real-life applications because of its simplicity and good performance both in theory and practice. However, in large-scale problems, where huge training data are available and must be used, such as road sign detection, the method’s training and test phases might be prohibitively demanding in terms of computations. Thus, for large-scale problems the reduction of computational complexity is essential.

Description: In order to accelerate both the training and test phases of kernel machines, it is proposed to map the input data to a randomized low-dimensional space wherein a feature selection algorithm is used and then existing fast linear methods are applied. The theory of the proposed method relies on a famous theorem in probability and harmonic analysis: Bochner’s Theorem. Based on this theorem one can show that any kernelized (shift-invariant) classifier can be, to an arbitrary accuracy, approximated by a linear classifier in the appropriate transformed space. Then, once the problem is re-posed in this space, significant computational improvements are achievable via feature selection because in general not all features are necessary for distinguishing one class from another and so a coarse approximation of the underlying kernel function results in a linear classifier having an experimental accuracy as good as the one of the original kernel classifier. Thus, a finite and small set of features is only used as the basis of the projection and, therefore, a significantly reduced dimensionality is achieved in the projection space. The algorithm, by Bochner’s Theorem, also achieves the linearization of the original nonlinear space of the data. These two properties, reduced dimensionality and linearization, lead to computational simplification in the training as well as the testing of a classifier. The speed improvement of this approach is experimentally shown on simple data sets and on an application to road sign detection.

Approximately 110 Fourier features are enough to approximate the SVM performance which corresponds 40x speed improvement in comparison to the number of features SVM used originally. — Approximately 110 Fourier features are enough to approximate the SVM performance which corresponds to 40-time speed improvement in comparison to the number of features SVM used originally.

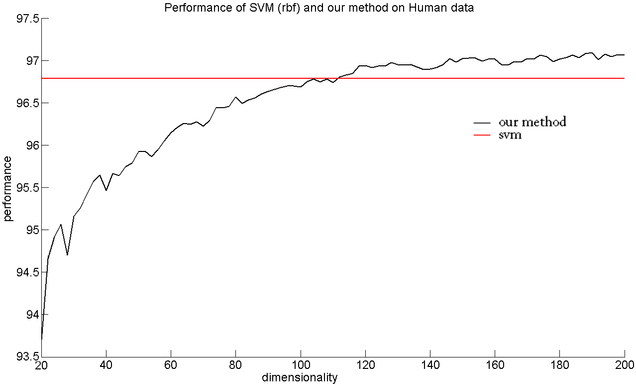
Results: It is experimentally shown that with either no or little performance loss, as compared to that of the original SVM algorithm, significant speed improvements are gained via the proposed method. For a synthetic data set (banana data set), the proposed algorithm is 25 times faster in the test phase and for a real data set (human detection data) it is 40 times faster.

Publications:

H. Ozkan, “Fast support vector machines using random Fourier features,” Tech. Rep. 2009-08, Boston University, Dept. of Electr. and Comp. Eng., Dec. 2009.