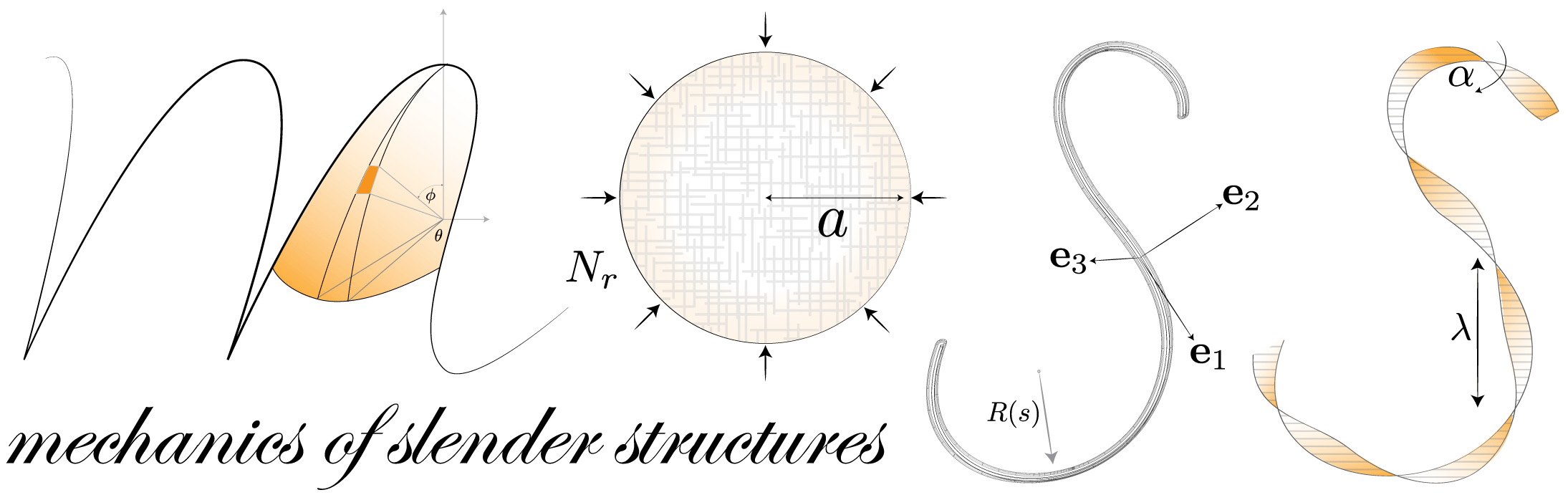
Research
Our group’s research is at the interface between structural mechanics and soft matter physics. We study large shape changes, pattern formation, and instabilities. If you are interested in these topics, I encourage you to read a review article from our group entitled “Elasticity and Stability of Shape-Shifting Structures”.
Books, Reviews, & Commentary

Germain Curvature: The Case for Naming the Mean Curvature of a Surface after Sophie Germain
arχiv, 2403622, (2023)
Essay: [arχiv]

Elasticity and Stability of Shape-Shifting Structuress
Current Opinion in Colloid & Interface Science, 40, 118-137, (2019)
Review: [Journal]

A Cut Above: Folding and Cutting Advanced Materials
Matter, 2403622, (2019)
Invited Commentary: [Journal]

Growing and Morphing Shapes: Using Swelling and Geometry to Control the Shape of Soft Materials
Active Matter, Ch. 18, 151-156, MIT Press, (2017)
Photo Credits: A. Bade, P.T. Brun, H. Hwang, M. Pezzulla, and M. Steranka
Mechanical Metamaterials
Mechanical metamaterials are complex structures that perform operations by utilizing nonlinearities and instabilities in a functional way. Structural instabilities, like buckling and snapping, provide ways to change the state of a structure (either locally or globally), creating patterns and switches. Origami and kirigami use geometric and topological nonlinearities – such as creases and cuts – as building blocks to enhance stretchability, create auxetic materials, design linear actuators, and build robotic grippers.

Mechanical Computing with Transmissive Snapping of Kirigami Shells
Advanced Functional Materials, 2403622, (2024)
Paper: [Journal]

The Collective Snapping of a Pair of Bumping Buckled Beams
Extreme Mechanics Letters, 2403622, (2024)

Self-Ordering of Buckling, Bending, and Bumping Beams
Physical Review Letters, 2403622, (2023)
Paper: [Journal][arχiv]
Press: [Physics]

Grasping with Kirigami Shells
Science Robotics, 6, eabd6426, (2021)
Paper: [Journal]
Press: [IEEE: Soft Robotics Podcast][Mecharithm][CNET][Futurity][The Spoon][BU The Brink]

Multistable Kirigami for Tunable Architected Materials
Physical Review Materials, 2, 110601(R), (2018)
Paper: [Journal]
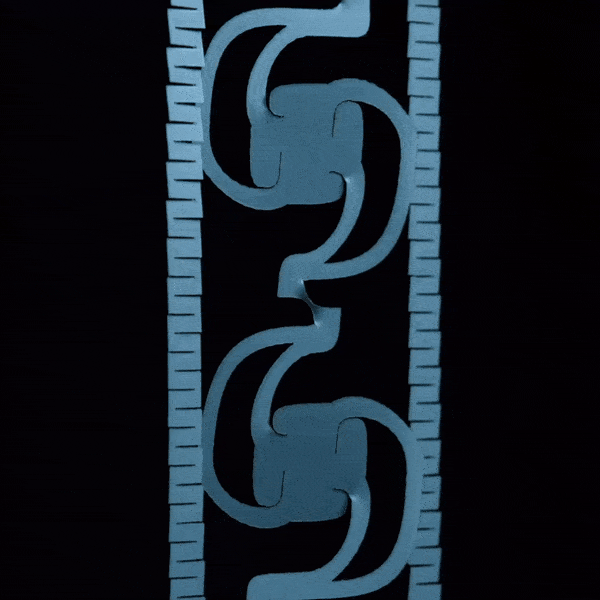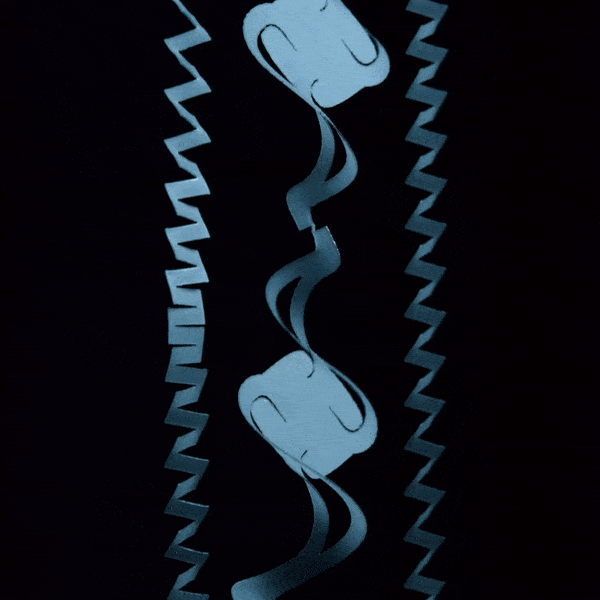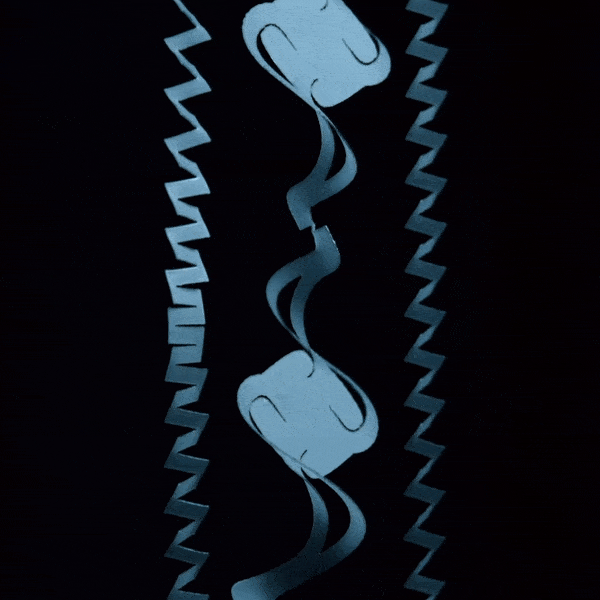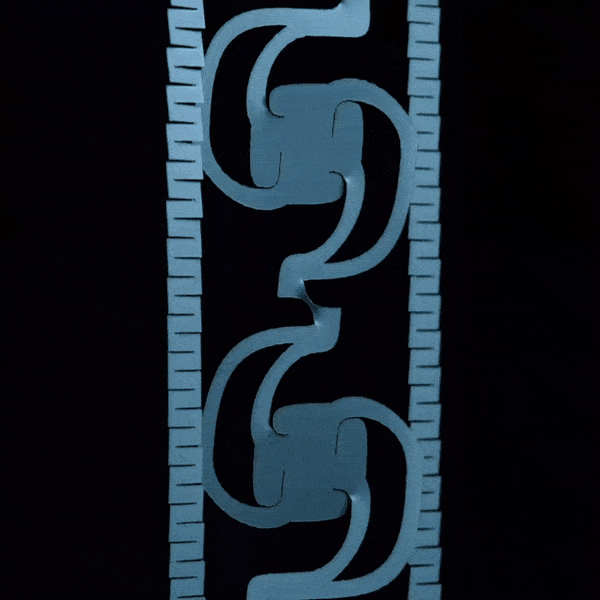
Kirigami Actuators
Soft Matter, 13, 9087–9092, (2017)
Paper: [Journal]
Elastogranular Structures
When elastic structures (fibers, string, plant roots, filaments) are combined with granular matter (soil, rocks, sand) it can create elastogranular structures that gain functionality through the interplay between structural instabilities and granular jamming. Because these elastogranular composites can bear significant loads, they could therefore provide natural barriers to sand and soil erosion, provide critical infrastructure that can morph and adapt, and create scaffolds for vegetal and coral growth. The combination of slender elastic structures with granular materials can produce elastogranular structures that can either jam into a rigid structural form capable of bearing significant loads, or be remarkably fragile and flow like a fluid for recyclability and reversability. This unprecedented reconfigurability and range of mechanical behaviors has the potential to create a new paradigm for the development of functional materials and adaptable structures, for instance, by creating structures with a reconfigurable granular skeleton embedded within soft materials.

Elastogranular Sheets
Matter, 6(4), 1217-1230, (2023)
Paper: [Journal]
Code: [GitHub: LAMMPSStructures]
Commentary: [Matter: Perspective]

Elastogranular Columns and Beams
Soft Matter, 18, 8262-8270, (2022)
Paper: [Journal]
Commentary: [Editorial Board: Highlighted Papers of 2022]

Emergence of Structure in Columns of Grains and Elastic Loops
Soft Matter, 17, 7662–7669, (2021)
Paper: [Journal]

Packing Transitions in the Elastogranular Confinement of a Slender Loop
Soft Matter, 16, 2039–2044, (2020)

Elastogranularity in Binary Granular Mixtures
Granular Matter, 22:3, (2020)

Superjammed: Tunable and Morphable Spanning Structures Through Granular Jamming
Technology|Architecture + Design, 4:2, 211-220, (2020)
Paper: [Journal]

Elastogranular Mechanics: Buckling, Jamming, and Structure Formation
Physical Review Letters, 120, 078002, (2018)

Buckling of Elastic Beams Embedded in Granular Media
Extreme Mechanics Letters, 9, 237-244, (2016)
Paper: [Journal]
Fundamental Mechanics of Slender Structures
The geometry and topology of thin structures dictates how they deform – it is easy to role a sheet of paper into a cylinder, but impossible to wrap it around a sphere without crumpling it, as this requires you to stretch it. A comparison of the energies for stretching and bending suggests that, if possible, a thin sheet will deform in a manner that avoid stretching as much as possible.

Stimuli-Responsive Shell Theory
Mathematics and Mechanics of Solids, 1-36, (2023)
Paper: [Journal]

Wrinkling and Developable Cones in Centrally Confined Sheets
Physical Review E, 108, 035002, (2023)

Efficient Snap-Through of Spherical Caps by Applying a Localized Curvature Stimulus
The European Physics Journal E (EPJE) , 45(3), (2022)
Paper: [Journal][arχiv]
Press: [EPJE Highlight]

Delayed Buckling of Spherical Shells due to Viscoelastic Knockdown of the Critical Load
Proceedings of the Royal Society A, 477(3), 20210253, (2021)

Nonlinear Buckling Behavior of a Complete Spherical Shell Under Uniform External Pressure and Homogeneous Natural Curvature
Physical Review E, 102, 023003 (2020)

Buckling of Geometrically Confined Shells
Soft Matter, 15, 1215–1222, (2019)
Paper: [Journal]

Evolution of Critical Buckling Conditions in
Imperfect Bilayer Shells through Residual Swelling
Soft Matter, 15, 6134–6144, (2019)
Paper: [Journal]

Static Bistability of Spherical Caps
Proceedings of the Royal Society A, 474, 20170910, (2017)

Bioinspired Electrically Activated Soft Bistable Actuators
Advanced Functional Materials, 1802999, (2018)
Paper: [Journal]

Curvature-Induced Instabilities of Shells
Physical Review Letters, 120, 048002, (2018)

Snapping of Bistable, Prestressed Cylindrical Shells
Europhysics Letters (EPL), 122, 64003, (2018)

Curvature-Driven Morphing of non-Euclidean Shells
Proceedings of the Royal Society A, 473, 20170087, (2017)

Geometry and Mechanics of Thin Growing Bilayers
Soft Matter, 12, 4435–4442, (2016)
Paper: [Journal]

Morphing of Geometric Composites via Residual Swelling
Soft Matter, 11, 5812–5820, (2015)
Paper: [Journal]

Falling Vertical Chain of Oscillators, Including Collisions, Damping, and Pretensioning
Journal of Sound and Vibration, 349, 195–205, (2015)

Dynamics of snapping beams and jumping poppers
Europhysics Letters (EPL), 105, 24001, (2014)

Equilibria and Instabilities of a Slinky: Discrete model
International Journal of Non-Linear Mechanics, 65, 236–244, (2014)

Draping Films: A Wrinkle to Fold Transition
Physical Review Letters, 105, 038303 (2010)
Paper: [Journal]
Interfacial Mechanics
Swelling of Gels and Rubber
When fluid comes into contact with an elastic network, it may infiltrate the material, causing it to significantly increase in size in order to absorb the fluid. The network is made of long polymer chains which form compact coils between crosslinks in the absence of fluid. As fluid is absorbed, the coils straighten out, decreasing their entropy in order to allow these fluid and solid to mix. During the swelling process, significant stress gradients can develop as the fluid diffuses through the material. This differential swelling can induce large, nonlinear deformations in slender structures.

Rising Beyond Elastocapillarity
Soft Matter, 12, 4886–4890, (2016)
Paper: [Journal]
What’s Going On Here? Two rubber fibers are dipped into a bath of oil. The oil rises via capillary action – surface tension draws the fluid up while gravity pulls it down. The fibers are flexible, so the surface tension bends them closer together – the same way that long, wet hair clumps together. As the oil begins to swell the rubber fibers, they bend to accomodate the difference in length between the wet and dry sides of the fiber. So there are two competing effects – surface tension pulling the fibers together, and swelling curling them apart.

Swelling-Induced Deformations: A Materials-Defined Transition from Macroscale to Microscale Deformations
Soft Matter, 9, 5524–5528, (2013)
Paper: [Journal]

Bending and Twisting of Soft Materials by Non-Homogenous Swelling
Soft Matter, 7, 5188–5193, (2011)
Paper: [Journal]

Crumpled Surface Structures
Soft Matter, 4, 82-85 (2008)
Paper: [Journal]

Snapping Surfaces
Advanced Materials, 19, 3589–3593, (2007)
Paper: [Journal]
Fluid-Structure Interactions

Extended Lubrication Theory: Improved Estimates of Flow in Channels with Variable Geometry
Proceedings of the Royal Society A, 473, 20170234, (2017)
Paper: [Journal]

Voltage-Induced Buckling of Dielectric Films using Fluid Electrodes
Applied Physics Letters, 108, 112901, (2016)
Paper: [Journal]

Buckling of Dielectric Elastomeric Plates for Soft, Electrically Active Microfluidic Pumps
Soft Matter, 10, 4789, (2014)
Paper: [Journal]

Control and Manipulation of Microfluidic Flow via Elastic Deformations
Soft Matter, 9, 7049–7053, (2013)
Paper: [Journal]
Solid-Solid Interfaces: Adhesion and Friction

Swelling Effects on Localized Adhesion of an Elastic Ribbon
Proceedings of the Royal Society A, 475, 20190067, (2019)
Paper: [Journal]

Revisiting the Generalized Scaling Law for Adhesion: Role of Compliance and Extension to Progressive Failure
Soft Matter, 13, 7529–7536, (2017)
Paper: [Journal]

Friction of Extensible Strips: An Extended Shear Lag Model with Experimental Evaluation
International Journal of Solids and Structures, 124, 125–134, (2017)
Paper: [Journal]
Biomechanics and Morphogenesis

Elastic Instabilities Govern the Morphogenesis of the Optic Cup
Physical Review Letters, 127, 138102 (2021)
Paper: [Journal]

Mechanics of Surface Area Regulation in Cells Examined with Confined Lipid Membranes
Proceedings of the National Academy of Sciences, 108(22), 9084–9088, (2011)
Paper: [Journal]
Publication List
(45.) J.–H. Lee, H.S. Park, and D.P. Holmes, “Stimuli-Responsive Shell Theory,” Accepted: Mathematics and Mechanics of Solids, (2023).
(44.) A. Guerra, A. Slim, D.P. Holmes, and O. Kodio, “Self–Ordering of Buckling, Bending, and Bumping Beams,” Physical Review Letters, 130, 148201, (2023). [Physics]
(43.) A. Guerra and D.P. Holmes, “Elastogranular Sheets”. Matter, 6(4), 1217–1230, (2023). [code] [Matter: Perspective]
(42.) A. Guerra, C. Lautzenhiser, X. Jiang, K. Flanagan, D. Rak, S. Tibbits, and D.P. Holmes, “Elastogranular Columns and Beams.” Soft Matter, 18, 8262– 8270, (2022). (Editorial Board: Highlighted Papers of 2022)
(41.) L. Stein–Montalvo, J.-H. Lee, Y. Yang, M. Landesberg, H.S. Park, and D.P. Holmes, “Efficient snap-through of spherical caps by applying a localized curvature stimulus,” European Physical Journal E (EPJE), 45:3, 1–11, (2022). [EPJE Highlight]
(40.) J.–H. Lee, H.S. Park, and D.P. Holmes, “Elastic Instabilities Govern the Morphogenesis of the Optic Cup,” Physical Review Letters, 127, 138102, (2021).
(39.) A. Guerra and D.P. Holmes, “Emergence of Structure in Columns of Grains and Elastic Rods”. Soft Matter, 17, 7662, (2021). [Random Walk Podcast][BU Engineering]
(38.) L. Stein–Montalvo, D.P. Holmes, and G. Coupier “Delayed buckling of spherical shells due to viscoelastic knockdown of the critical load,” Proceedings of the Royal Society A, 477, 20210253, (2021).
(37.) Y. Yang, K. Vella, and D.P. Holmes, “Grasping with Kirigami Shells,” Science Robotics, 6, eabd6426, (2021). [IEEE: Soft Robotics Podcast][Mecharithm][CNET][Futurity][The Spoon][BU The Brink]
(36.) Z. Cohen, N. Elberfeld, A. Moorman, J. Laucks, S. Kernizan, D.P. Holmes, and S. Tibbits, “Superjammed: Tunable and Morphable Spanning Structures Through Granular Jamming”, Technology | Architecture + Design (TAD), 4:2, 211–220, (2020).
(35.) D.P. Holmes, J.H. Lee, H.S. Park, and M. Pezzulla, “The nonlinear buckling behavior of a complete spherical shell under uniform external pressure and homogenous natural curvature,” Physical Review E, 102, 023003, (2020). [arXiv] [Mathematica]
(34.) D.J. Schunter Jr., R.K. Czech, and D.P. Holmes, “Packing Transitions in the Elastogranular Confinement of a Slender Loop,” Soft Matter, 16, 2039–2044, (2020).
(33.) D.J. Schunter Jr., M. Boucher, and D.P. Holmes, “Elastogranularity in Binary Granular Mixtures,” Granular Matter, 22:3, (2020).
(32.) A. Lee, D. Yan, M. Pezzulla, D.P. Holmes, and P.M. Reis, “Evolution of critical buckling conditions in imperfect bilayer shells through residual swelling,” Soft Matter, 15, 6134-6144, (2019).
(31.) M. Curatolo, P. Nardinocchi, L. Teresi, and D.P. Holmes, “Swelling effects on localized adhesion of an elastic ribbon,” Proceedings of the Royal Society A, 475(2225), 67, (2019). [PDF]
(30.) D.P. Holmes, “Elasticity and Stability of Shape Changing Structures,” Current Opinion in Colloid and Interface Science, 40:118-137, (2019). [PDF] [arXiv]
(29.) L. Stein-Montalvo, P. Costa, M. Pezzulla, D.P. Holmes, “Buckling of geometrically confined shells,” Soft Matter, 15(6), 1215-1222, (2019). [PDF] [arXiv]
Special Issue: Emerging Investigators
Front Cover
(28.) Y. Yang, M.A. Dias, and D.P. Holmes, “Multistable Kirigami for Tunable Architected Materials,” Physical Review Materials, 2, 110601(R), (2018). [PDF] [arXiv]
(27.) X. Jiang, M. Pezzulla, H. Shao, T.K. Ghosh, and D.P. Holmes, “Snapping of bistable, prestressed cylindrical shells,” Europhysics Letters (EPL), 122(6), (2018). [Link] [arXiv]
(26.) S. Wei, H. Shao, X. Jiang, D.P. Holmes, and T.K. Ghosh, “Bioinspired Electrically Activated Soft Bistable Actuators,” Advanced Functional Materials, 1802999, (2018). [Link]
(25.) M. Taffetani, X. Jiang, D.P. Holmes, and D. Vella, “Static Bistability of Spherical Caps,” Proceedings of the Royal Society A, 474(2213), (2018). [Link] [arXiv]
(24.) D.J. Schunter Jr., M. Brandenbourger, S. Perriseau, and D.P. Holmes, “Elastogranular Mechanics: Buckling, Jamming, and Structure Formation,” Physical Review Letters, 120, 078002, (2018). [PDF] [arXiv][Soft Bites]
Front Cover
(23.) M. Pezzulla, N. Stoop, M.P. Steranka, A.J. Bade, and D.P. Holmes, “Curvature-Induced Instabilities of Shells,” Physical Review Letters, 120, 048002, (2018). [PDF] [arXiv]
(22.) M.A. Dias, M.P. McCarron, D. Rayneau-Kirkhope, P.Z. Hanakata, D.K. Campbell, H.S. Park, and D.P. Holmes, “Kirigami Actuators,” Soft Matter, 13, 9087-9802, (2017). [PDF] [arXiv]
Back Cover: [Link]
(21.) A.R. Mojdehi, D.P. Holmes, and D.A. Dillard, “Revisiting the Generalized Scaling Law for Adhesion: Role of Compliance and Extension to Progressive Failure,” Soft Matter, 13, 7529-7536, (2017). [PDF]
(20.) B. Tavakol, D.P. Holmes, G. Froehlicher, and H.A. Stone, “Extended Lubrication Theory: Estimation of Fluid Flow in Channels with Variable Geometry,” Proceedings of the Royal Society A, 474, 0234, (2017).[PDF] [arXiv]
(19.) A.R. Mojdehi, D.P. Holmes, and D.A. Dillard, “Friction of extensible strips: An extended shear lag model with experimental evaluation,” International Journal of Solids and Structures, (2017). [PDF]
(18.) M. Pezzulla, N. Stoop, X. Jiang, and D.P. Holmes, “Curvature-Driven Morphing of Non-Euclidean Shells,” Proceedings of the Royal Society A, 473(2201), (2017). [Link] [arXiv]
(17.) A.R. Mojdehi, B. Tavakol, W. Royston, D.A. Dillard, D.P. Holmes, “Buckling of elastic beams embedded in granular media,” Extreme Mechanics Letters, 9, 237-244, (2016). [PDF]
(16.) D.P. Holmes, P.-T. Brun, A. Pandey, and S. Protière, “Rising beyond elastocapillarity,” Soft Matter, 12, 4886-4890, (2016). [PDF]
Front Cover: [Link]
(15.) M. Pezzulla, G.P. Smith, P. Nardinocchi, and D.P. Holmes, “Geometry and Mechanics of Thin Growing Bilayers,” Soft Matter, 12, 4435-4442, (2016). [PDF] [arXiv]
(14.) B. Tavakol and D.P. Holmes, “Voltage-Induced Buckling of Dielectric Films using Fluid Electrodes,” Applied Physics Letters, 108, 112901 (2016).[PDF] [arXiv]
(13.) M. Pezzulla, S.A. Shillig, P. Nardinocchi, and D.P. Holmes, “Morphing of Geometric Composites via Residual Swelling,” Soft Matter, 11, 5812-5820, (2015). [PDF] [arXiv]
Inside Cover: [Link]
(12.) R.H. Plaut, A.D. Borum, D.P. Holmes, and D.A. Dillard, “Falling vertical chain of oscillators, including collisions, damping, and pretensioning,” Journal of Sound and Vibration, 349, 195-205, (2015). [PDF]
(11.) D.P. Holmes, A.D. Borum, B.F. Moore III, R.H. Plaut, and D.A. Dillard, “Equilibria and Instabilities of a Slinky: Discrete Model”, International Journal of Nonlinear Mechanics, 65, 236-244, (2014). [PDF] [arXiv]
(10.) B. Tavakol, M. Bozlar, C. Punckt, D.P. Holmes, G. Froehlicher, H.A. Stone, I.A. Aksay, and D.P. Holmes, “Buckling of Dielectric Elastomeric Plates for Soft, Electrically Active Microfluidic Pumps “, Soft Matter, 10(27), 4789-4794, (2014). [PDF]
(9.) A. Pandey, D.E. Moulton, D. Vella, and D.P. Holmes, “Dynamics of Snapping Beams and Jumping Poppers”, EPL (Europhysical Letters), 105, 24001, (2014). [PDF] [arXiv]
(8.) A. Pandey and D.P. Holmes, “Swelling-Induced Deformations: A Materials-Defined Transition from Macroscopic to Microscopic Deformations,” Soft Matter, 9, 5524, (2013). [PDF]
(7.) D.P. Holmes, B. Tavakol, G. Froehlicher, and H.A. Stone, “Control and Manipulation of Microfluidic Fluid Flow via Elastic Deformations”, Soft Matter, 9, 7049, (2013). [PDF]
Special Issue: Emerging Investigators [PDF]
(6.) D.P. Holmes, “Elastic Instabilities for Form and Function”, iMechanica, (2012). [Link]
(5.) D.P. Holmes, M. Roché, T. Sinha, and H.A. Stone, “Bending and Twisting of Soft Materials by Non-Homogenous Swelling,” Soft Matter, 7, 5188, (2011). [PDF]
(4.) M. Staykova, D.P. Holmes, C. Read, and H.A. Stone, Proc. Natl. Acad. Sci, 108(22), 9084-9088, (2011). [PDF]
(3.) D.P. Holmes and A.J. Crosby, “Draping Films: A Wrinkle to Fold Transition,” Physical Review Letters, 105, 038303, (2010). [PDF]
(2.) D.P. Holmes, M. Ursiny, and A.J. Crosby, “Crumpled Surface Structures,” Soft Matter, 4, 82, (2008). [PDF]
(1.) D.P. Holmes and A.J. Crosby, “Snapping Surfaces,” Advanced Materials, 19, 3589, (2007). [PDF]