Development of Mathematical and Computational Methods for Improved Protein-Protein Docking
Vajda, Kozakov, Paschalidis, and Vakili groups
Supported by:
NIH R01 GM061867 “A multistage approach to protein-protein docking” (PI: Vajda)
NIH R01 GM093147 “Refinement Methods for Protein Docking based on Exploring Multi-Dimensional Energy Funnels” (PI: Paschalidis and Kozakov)
NSF DBI 1147082 “ABI Development: Refinement Algorithms and Server for Protein Docking” (PI: Vajda and Kozakov)
Protein-protein interactions play a central role in various aspects of the structural and functional organization of the cell, and their elucidation is crucial for a better understanding of processes such as metabolic control, signal transduction, and gene regulation. Genome-wide proteomics studies, primarily yeast two-hybrid assays, will provide an increasing list of interacting proteins, but only a small fraction of the potential complexes will be amenable to direct experimental analysis. Thus, it is important to develop docking methods that can elucidate the details of specific interactions at the atomic level.
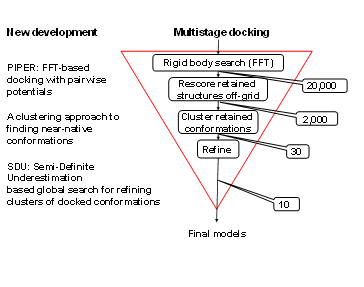
The Vajda group has developed a multistage approach to protein-protein docking (Figure 1). The procedure starts with the rigid body docking program PIPER. PIPER performs exhaustive evaluation of an energy function in discretized 6D space of mutual orientations of two proteins. We sample 70,000 rotations which approximately correspond to sampling at every 5 degrees in the space of Euler angles. In the translational space the sampling is defined by the 1.2 Å grid cell size. The energy-like scoring function describing the receptor-ligand interactions is defined on this grid and is efficiently calculated using Fast Fourier transforms. The novelty of the PIPER algorithm is that the scoring function includes a pairwise structure-based interaction potential. Results are clustered, and up to the 30 largest clusters are retained for refinement (see below). These calculations are implemented in the protein-protein docking server ClusPro, regularly used by over 4000 research groups worldwide. The server runs over 1000 docking jobs each month, and models obtained by ClusPro has been so far published and analyzed in over 200 papers. In addition, ClusPro is consistently the best protein docking server, as shown by the results of CAPRI, the ongoing worldwide protein docking experiment.
The ongoing collaboration between the Vajda, Kozakov, Paschalidis, and Vakili groups focuses on the refinement of the models generated by ClusPro. Since refinement is computationally very demanding, methods that can used on a server required the development of novel and very efficient approaches. We made substantial progress toward achieving the goal of a computationally feasible refinement, and developed three innovative algorithms as follows.
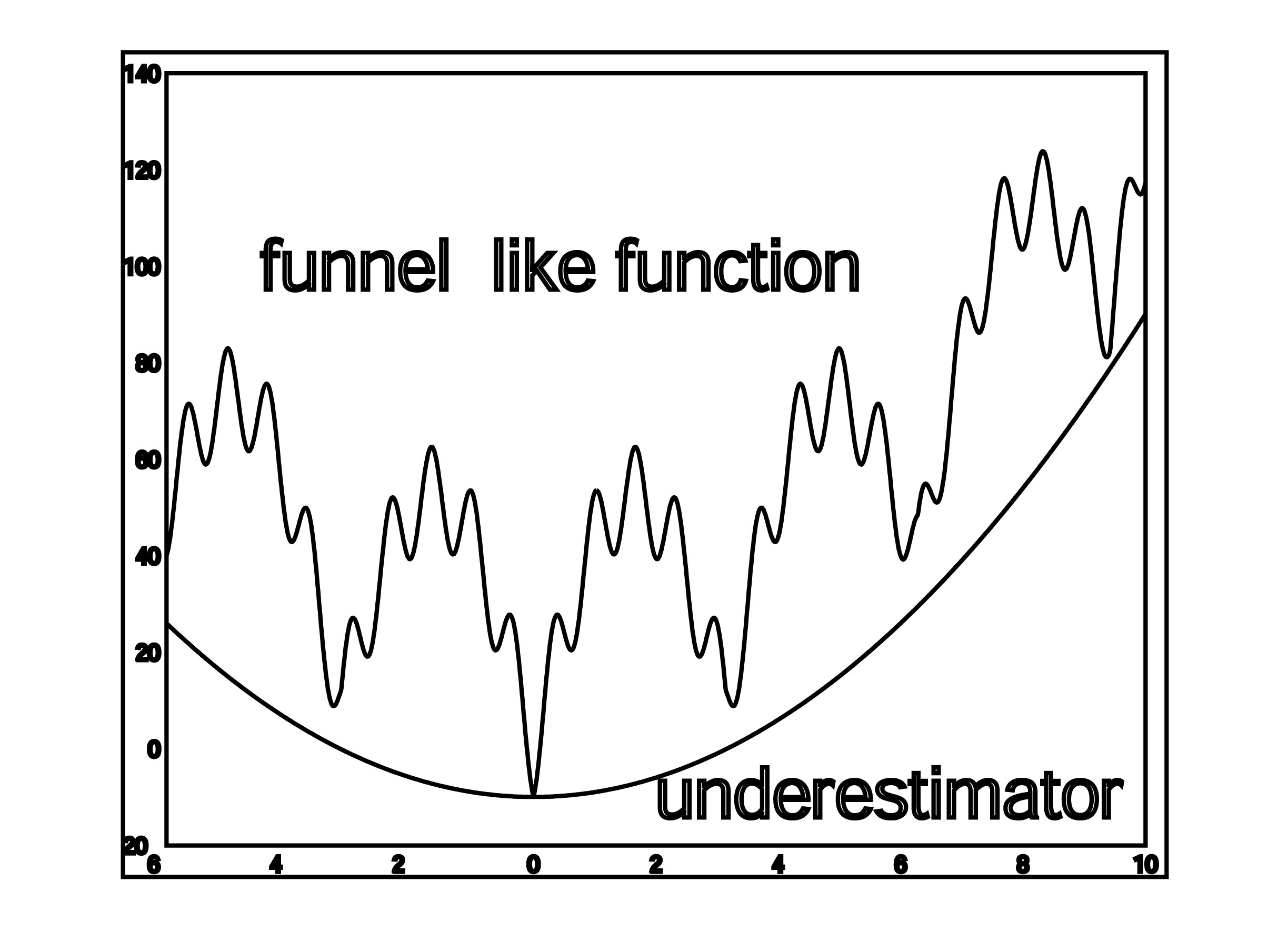
- SDU (Semi-Definite programming based Underestimation. SDU is a stochastic global optimization method based on the assumption that the free energy, ΔG, is a funnel-like function within the region defined by each cluster (Paschalidis et al., 2007). Given a set of K local minima x1,…,xK of ΔG, we construct a convex quadratic function U(x) = x′Qx + b′x + c that underestimates ΔG at all local minima i.e., U(xi) ≤ ΔG(xi), i = 1, . . . ,K. The underestimator U(x) can be found by solving a semi-definite programming problem. Assuming that U(x) reflects the funnel-like behavior of free energy function, we call the global minimum xP of U the “predictive conformation”, where xP = −(1/2)Q−1b. We bias sampling toward xP by selecting points from the probability density function proportional to –U. The new points are used as starting states in local energy minimization, and then added to the set of local minima. High energy samples or those far from xP are discarded. If there is no progress in reducing the minimum energy over several iterations then the algorithms is terminated. The SDU algorithm has been used with success in the latest rounds of the CAPRI experiment.
- A New distributed algorithm for side-chain positioning in the process of protein docking. Refinement requires adjusting the side chain conformations in the interface as the two proteins interact, and thus side-chain positioning (SCP) is an important component of computational protein docking methods. Existing SCP methods and available software have been designed for protein folding applications and do not take into account the significant special structure that SCP for docking exhibits. We have developed a new algorithm, which poses SCP as a Maximum Weighted Independent Set (MWIS) problem on an appropriately constructed graph. The approach solves a relaxation of the MWIS and then rounds the solution to obtain a high-quality feasible solution to the problem. The algorithm is fully distributed and can be executed on a large network of processing nodes requiring only local information and message-passing between neighboring nodes. Motivated by the special structure in docking, we have established optimality guarantees for a certain class of graphs. Our results on a benchmark set of protein complexes show that the predictions are close to the native structure and that the new method has some advantages over existing side-chain prediction tools.
- Rigid body energy minimization on manifolds. We have developed efficient rigid-body optimization algorithm that, compared to the most widely used algorithms, converges approximately an order of magnitude faster to conformations with equal or slightly lower energy. The space of rigid body transformations is a nonlinear manifold, namely, a space that locally resembles a Euclidean space. We use a canonical parametrization of the manifold, called the exponential parametrization, to map the Euclidean tangent space of the manifold onto the manifold itself. Thus, we locally transform the rigid body optimization to an optimization over a Euclidean space where basic optimization algorithms are applicable. Compared to commonly used methods, this formulation substantially reduces the dimension of the search space. As a result, it requires far fewer costly function and gradient evaluations and leads to a more efficient algorithm. We have selected a quasi-Newton method for local optimization since it uses only gradient information to obtain second order information about the energy function, and avoids the far more costly direct Hessian evaluations.
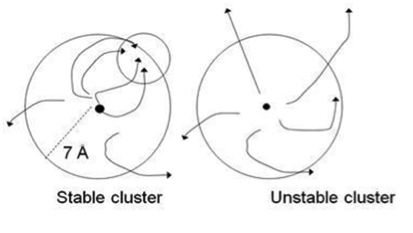
The side chain search and rigid body minimization algorithms are being implemented into a computationally efficient Monte Carlo minimization method that will enable us to carry out refinement and final model selection by applying stability analysis to each cluster obtained by ClusPro. Stability analysis is based on the hypothesis that clusters of near-native structures are located in broad energy funnels. This hypothesis is tested by starting short Monte Carlo minimization (MCM) simulations from randomly selected structures of the cluster. Each simulation step includes both repacking of the interface side chains and rotational/translational moves. Convergence for a substantial fraction of MCM trajectories to a region within the cluster indicates a broad funnel, and the point of convergence provides an improved estimate of the native structure. Conversely, diverging trajectories indicate that a substantive free energy funnel does not exist (Fig. 3), and hence the cluster is not near-native.