Research Areas & Projects
Waves in Complex Photonic Media
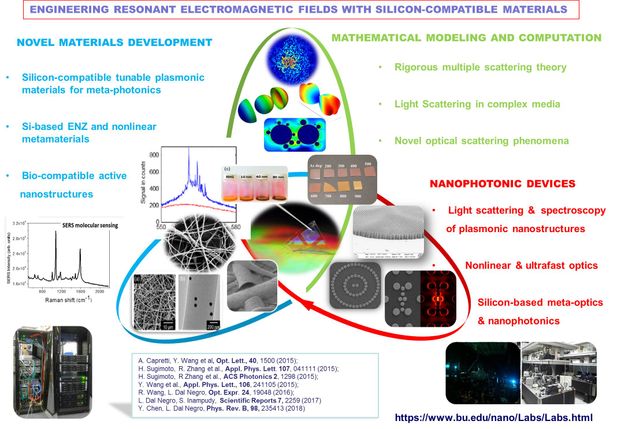
The control of nanomaterials, structures and optical fields lies at the heart of the current nanotechnology revolution and offers unprecedented opportunities to engineer novel functional elements on the nanoscale. Dal Negro’s group research activities are focused on the nanofabrication, linear/nonlinear optical characterization and electromagnetic modeling of metal-dielectric nanomaterials and nanostructures for on-chip nanophotonics applications. In particular, we develop efficient nanoscale light sources and laser structures based on the cost-effective silicon technology and we study the behavior of optical fields confined in complex media such as fractals, quasi-crystals and more complex deterministic aperiodic systems. Our combined computational and experimental activities aim at advancing the fields of silicon photonics and nanoplasmonics by demonstrating novel concepts and device structures for on-chip optical sensing, light emission, energy conversion and thin-film solar cell technology.
In particular, we fabricate semiconductor and optical bio-polymers nanostructures, metal nanoparticle arrays and we investigate their linear and nonlinear optical properties. In addition, using electron-beam nanolithography we design and fabricate large-scale, resonant arrays of nanoparticles and we study their photonic-plasmonic behavior in relation to light-matter coupling, nonlinear optical response and the engineering of multiple light scattering and radiative processes (light emission) on the nanoscale. Moreover, our experimental research activities are assisted by rigorous electrodynamical modeling of complex photonic media based on efficient analytical models and numerical approaches to multiple scattering theories. The recent mathematical methods of deep learning and artificial neural networks are utilized in our group for the design of multiple scattering media with novel functionalities.
- Computationally-Guided Design of Energy Efficient Electronic Materials (CDE3M), ARmy Research Laboratory
Artificial Neural Networks (ANN) for photonics modeling and design
In this research activity we utilize state-of-the-art developments in machine learning and artificial neural networks for the design and modeling of complex photonic media and metamaterial structures. Specifically, we employ the emerging paradigm of physics-informed neural networks (PINNs)
for the solution of representative inverse scattering problems in photonic metamaterials and nano-optics technologies. For more information read our recent paper
Wave localization in aperiodic photonic media

Understanding wave transport and localization phenomena in aperiodic optical media provides opportunities to tailor their optical density of states and to enhance light-matter interactions for the engineering of novel active photonic devices. For instance, the study of multiple light scattering
in random media led to the demonstration of random lasers with both uniform and correlated disorder, as well as to remarkable advances in optical imaging and spectroscopy. Our research focuses on the design and engineering of complex photonic media that are deterministic in nature. A representative example of a deterministic aperiodic scattering array that plays a significant role in our research is shown in the Scanning Electron Microscope (SEM) picture above, which displays a Vogel spiral array of SiN nanopillars. More generally, deterministic structures with aperiodic though long-range ordered distributions of scattering potentials have a long history in the electronics and optics communities due to significant advantages in design and compatibility with standard fabrication technologies compared to random systems. These structures manifest unique spectral characteristics that lead to physical properties that cannot be found in either periodic or uniform random media, such as multifractal density of eigenstates with varying degrees of spatial localization, known as critical modes, anomalous photon transport regimes, and distinctive wave localization transitions. In the last 15 years our group has developed a large number of aperiodic deterministic systems for photonics applications that include light sources and lasers, optical biosensors, thin-film photovoltaic cells, and non-linear optical elements.
Recently we introduced a novel class of aperiodic photonic systems that leverage the distinctive aperiodic order, unpredictability, and complexity that is present in number theory. Examples include the aperiodic distribution of prime numbers and their algebraic field generalizations, the almost-periodicity characteristic of arithmetic functions, aperiodic primitive roots and quadratic residue sequences, the intricate behavior of Dirichlet L-functions (which include the Riemann’s zeta function), and the distribution of binary digits in Galois fields, just to name a few. Moreover, we recently demonstrated and engineered novel photonic structures that manifest the distinctive aperiodic order of elliptic curves and the associated discrete logarithm problem over finite fields. Our work not only underlines the importance of structural correlations in elliptic curve-based structures for photonics technology but additionally provides an optics-driven approach to rapidly identify the potential vulnerabilities of modern EC-based cryptosystems. In our research we combine the interdisciplinary methods of point patterns spatial statistics and spectral graph theory with the rigorous Green’s matrix solution of the multiple wave scattering problem for electric and magnetic dipoles and we systematically explore the spectral and light scattering properties of novel deterministic aperiodic structures with enhanced light-matter coupling for nanophotonics and metamaterials applications to imaging and spectroscopy.
Fractional calculus and photon transport in complex media
In this research project we use the recently developed mathematical tools of fractional calculus to describe anomalous transport phenomena in the presence of memory and long-range spatial correlations in aperiodic complex photonic media. In particular we work with fractional
transport equations with space and time derivatives of arbitrary (non-integer) order. These correspond to integro-differential operators
with power-law kernels that naturally account for space correlations and time memory effects established when wave excitations are multiply scattered in strongly non-homogeneous environments. Lately we applied these methods to random lasers with incoherent feedback, which are described within the diffusion approximation, and we extended the traditional Letokhov laser model by considering fractional
diffusion equations of arbitrary order, including distributed-order (DO) fractional diffusion processes. Our comprehensive analytical and numerical analysis of fractional photon transport regimes in deterministic aperiodic and random gain media demonstrates the relevance of engineered photon sub-diffusion processes to realize novel lasers and active device structures with strongly reduced amplification threshold
and footprint.
Novel resonant materials for metaphotonics
Metaphotonics is the convergence of plasmonics, metamaterials, and nonlinear optics on a single chip. In this context, we are developing
alternative plasmonic materials compatible with complementary metal-oxide-semiconductor (CMOS) technology and with tunable optical
responses, reduced optical losses, and low refractive indices that provide exciting opportunities for future nonlinear and active metaphotonic device applications. Refer to our publications page for additional details on these activities.
Plasmonics and metamaterials
We work on the design, synthesis, and experimental characterization of resonant metallo-dielectric nanostructures for plasmonics and metamaterials technology. In particular, we are interested in developing novel concepts that leverage strong modifications of electromagnetic fields in nanoscale environments for optical sensing and spectroscopy applications. Refer to our publications page for additional details on these activities.