Mechanics of Materials: Combined Loading
Thin-Walled Pressure Vessels
There are a multitude of industrial applications that require thin-shelled structures for the storage of pressurized gases and liquids. These pressure vessels help store propane, transport oil to refineries, and keep our basketballs inflated. The most common shapes you will encounter include cylindrical and spherical pressure vessels. Froem a simple static equilibrium force balance we can immediately deduce the stresses in these structures. We'll start with the normal stresses on the surface of a cylindrical shell. Because it is thin, we only need to consider stress on the surface of the structure. This assumption significantly simplifies the mathematics, and only leads to a predicted stress that is about 4% lower than the actual stress. We'll talk about this assumption of plane stress in more detail in the next lesson. For the surface of a cylinder, it doesn't make much sense to think about the x and y directions, it's easier to think about the longitudinal axis and the circumferential axis of the cylinder. The stress in the circumferential direction is often referred to as a hoop stress – it's the same stress you feel around your waist as you tighten your belt. Let's draw two free body diagrams by slicing the cylinder in half down the long axis and through the circumferential axis.
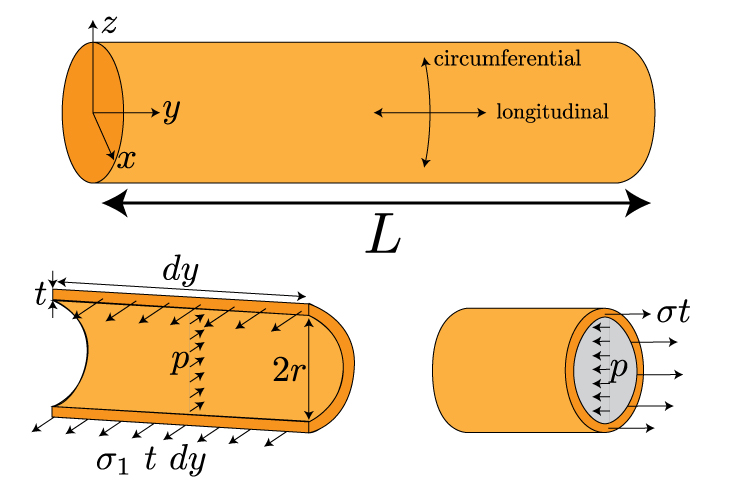
We'll denote sigma1 as the hoop stress and sigma2 as the longitudinal stress. A force balance in the x and y directions – found in part by multiplying the stress by the relevant area t dy – yields the following equations:
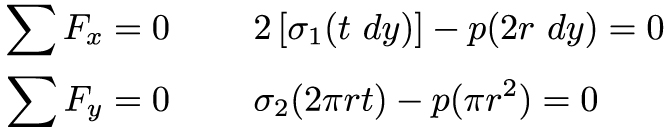
From these force balances, we can easily solve for the two principal stresses:

In both cases, the stress increases linearly with the internal (or external) pressure and the radius of the cylinder, and inversely with the shell thickness. We can apply the same process to a spherical shell. In the illustration below, we've sliced this shell in half:
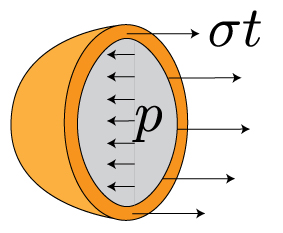
You'll note that the force balance looks just like the longitudinal stress in the cylindrical shell above. Since its spherical, the two principal stresses are the same, and the same as the longitudinal stress above:
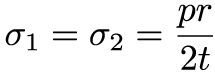
Combined Loading
Through these lessons, we have covered a variety of different means for generating normal and shear stresses in structures – pulling/pushing, bending, twisting, pressurizing. The various equations describing these stresses are all linear, and this has a very important consequence: these stresses can be simply added together to determine the total stress on an object because of the superposition principle. This gives us a powerful means for calculating the total normal and shear stress for complicated, combined loadings.
There are just a couple of rules to keep in mind:
- Normal stresses add only to other normal stresses, and shear stresses combine with shear stresses.
- Stresses add together if they're pointing in the same direction (i.e. sigmax + sigmax, or sigmay+sigmay)
Here's a helpful table of the normal and shear stresses we've discussed:

You'll notice that I've left the subscripts off the relevant stresses, moments, and moments of areas. The most difficult part of combined loading problems is identifying the direction of the stresses in the problem. I cannot emphasize this point enough: a good schematic (and sometimes a couple of good drawings) is the most important thing you can do while setting up these problems. Bending in multiple directions because multiple normal and shear forces is a very challenging thing to visualize. You will never regret taking the time to draw the loaded structure from multiple angles. There is really no other new content here, but that does not mean the problems you will encounter will be trivial. It will be best to see a few examples for how to calculate the stresses within structures under combined loading.
Summary
In this lesson, we introduced the stresses incurred from pressures exerted on thin-walled pressure vessels. We focused on two structures specifically: cylindrical and spherical shells. The force balance for these examples yielded principal stresses that act in longitudinal and circumferential directions on the shells. Additionally, we summarized all the relevant normal and shear stresses described in this course. These stresses are all linear, and can therefore be added together in the case of combined loading (like, bending a thin-walled pressure vessel). It's important to remember that normal stresses add together, and shear stresses add together. And, only stresses acting in the same direction can be added together.
 This material is based upon work supported by the National Science Foundation under Grant No. 1454153. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
This material is based upon work supported by the National Science Foundation under Grant No. 1454153. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.