Normal and shear stress, as we have defined them, are measures of the average stress over a cross section. Simply put, the magnitude of stress at any place along the cross section is the same. This means the load is distributed over the entire cross section. Alternatively, if the external force is focused over a small region, it is referred to as a point load. A point load, unlike a distributed load, causes stress near the point of loading to be much higher than the average stress.  This leads to very complicated deformations from very complicated states of stress. Describing this deformation is beyond the scope of this course. But, if you look at the illustrations of a distributed load vs. a point load below, what you will notice is that the deformations (and hence, the stress distributions) start to look similar once you get far away from the point load. 

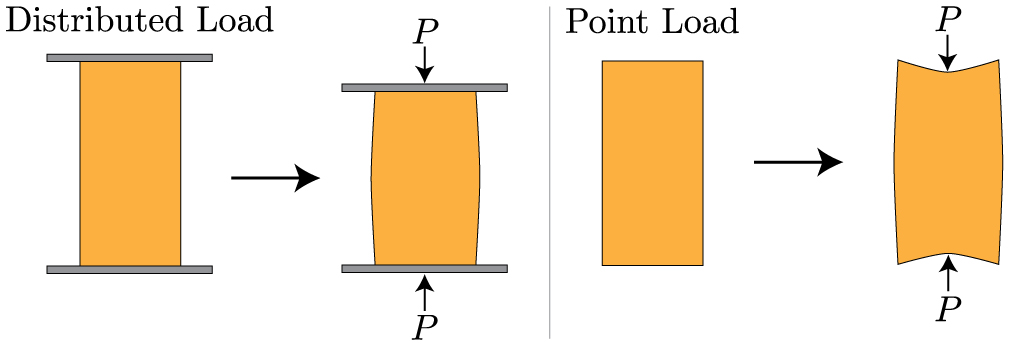
A natural question is: how far away from the point load does the stress become evenly distributed (i.e. when are we safe to use our average stress definition)? The Saint-Venant Principle states that the average stress approximation is valid within the material for all points that are as far away from the load as the structure is wide.  This statement may be easier to understand visually: 

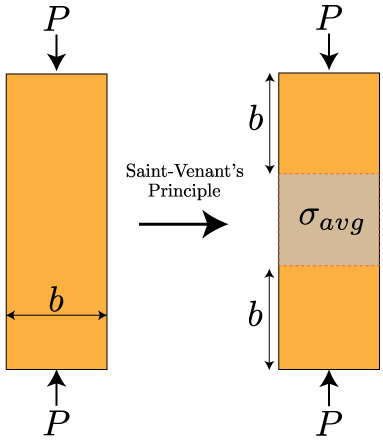
This principle is important – most of the material covered in this class assumes that the stress is evenly distributed (or, averaged) over the cross section. The Saint-Venant Principle allows us to quickly identify where in the structure this assumption is true. 

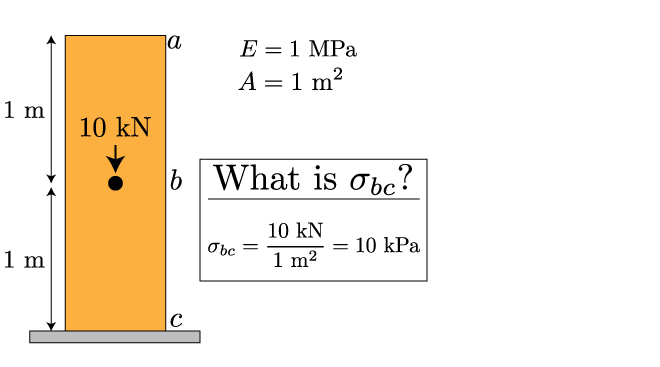
Let’s switch gears for a moment, and return to the connection between stress and strain. Until now, our approach has been: 1. determine the external forces from a statics analysis, 2. calculate the internal stress, and 3. use Hooke’s law to determine the strain. For instance, take the structure below and determine the stress at its center. You are given the applied force and the cross sectional area, and this becomes a simple calculation.

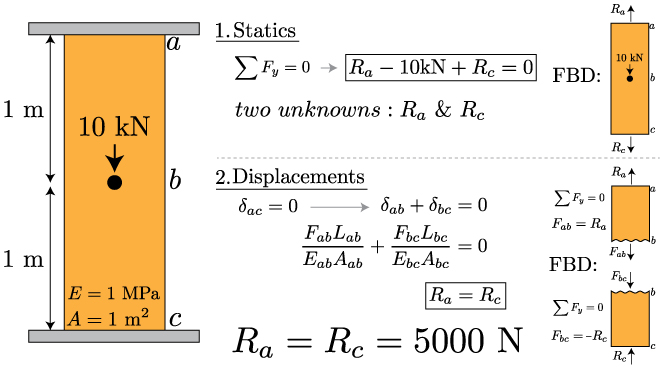
However, if the problem is changed slightly, solving it becomes a more tricky task. In the problem below, there is now a support at the top and bottom of the structure (assume that it's permanently attached at each edge). To understand why this gets complicated, take a look at the Free-Body Diagram. By summing the forces in the y-direction and setting them equal to zero, we see that we end up with one equation and two unknown reaction forces R_a & R_c. One equation, two unknowns… we need something else.  This type of problem is referred to as statically indeterminate, because you can't determine the answer to the problem by considering the statics alone. In all statically indeterminate problems, (and, these will be a recurring theme throughout the semester), we use the statics and the displacements together to determine the answer. So, what do we know about the displacements? Well, we know that the structure is stuck to the supports, so it can't move up or down. More specifically, the displacement of the between points a and c has to be zero. Now we can split the structure in half (because the load is applied at the center), and note that if the total displacement has to be zero, then the displacement of the top half (from a to b) plus the displacement of the bottom half (from b to c) has to be zero. Now we can use our equation for displacement superposition from the last lesson. Finally, from our second free body diagram, we can determine the relationships between the forces and unknown reactions. This results in our second equation containing our unknown reaction forces R_a & R_c. Two equations, two unknowns, we can solve these equations simultaneously, and determine our reaction forces.

We just looked at a specific example of a statically indeterminate problem. In general, a problem is statically indeterminate if a structure is held by more supports than are required to maintain equilibrium. This condition will always result in more unknown reaction forces than number of equilibrium equations.

In this lesson, we described the limitations on our assumption of an average stress distribution. We learned that Saint-Venant's Principle gives us a good estimate for when we can safely use our average stress assumption.

We also encountered statically indeterminate problems for the first time. These types of problems will occur throughout this class. They will always have the same identifying features: more unknown forces than the number of equilibrium equations determined by a statics analysis. They will always have the same procedure for solution: consider both the statics and the displacements of the structure.  In order to use structural displacement to help solve the problem, you'll need to ask yourself: "what do I know about the displacement of the structure?"