Category: Papers
Paper: Curvature-driven morphing of non-Euclidean shells
Curvature-driven morphing of non-Euclidean shells
Matteo Pezzulla, Norbert Stoop, Xin Jiang, Douglas P. Holmes, Proceedings of the Royal Society A, 473(2201), (2017).
Abstract: We investigate how thin structures change their shape in response to non-mechanical stimuli that can be interpreted as variations in the structure’s natural curvature. Starting from the theory of non-Euclidean plates and shells, we derive an effective model that reduces a three-dimensional stimulus to the natural fundamental forms of the mid-surface of the structure, incorporating expansion, or growth, in the thickness. Then, we apply the model to a variety of thin bodies, from flat plates to spherical shells, obtaining excellent agreement between theory and numerics. We show how cylinders and cones can either bend more or unroll, and eventually snap and rotate. We also study the nearly isometric deformations of a spherical shell and describe how this shape change is ruled by the geometry of a spindle. As the derived results stem from a purely geometrical model, they are general and scalable.
Link: http://rspa.royalsocietypublishing.org/content/473/2201/20170087

Paper: Elastogranular Buckling
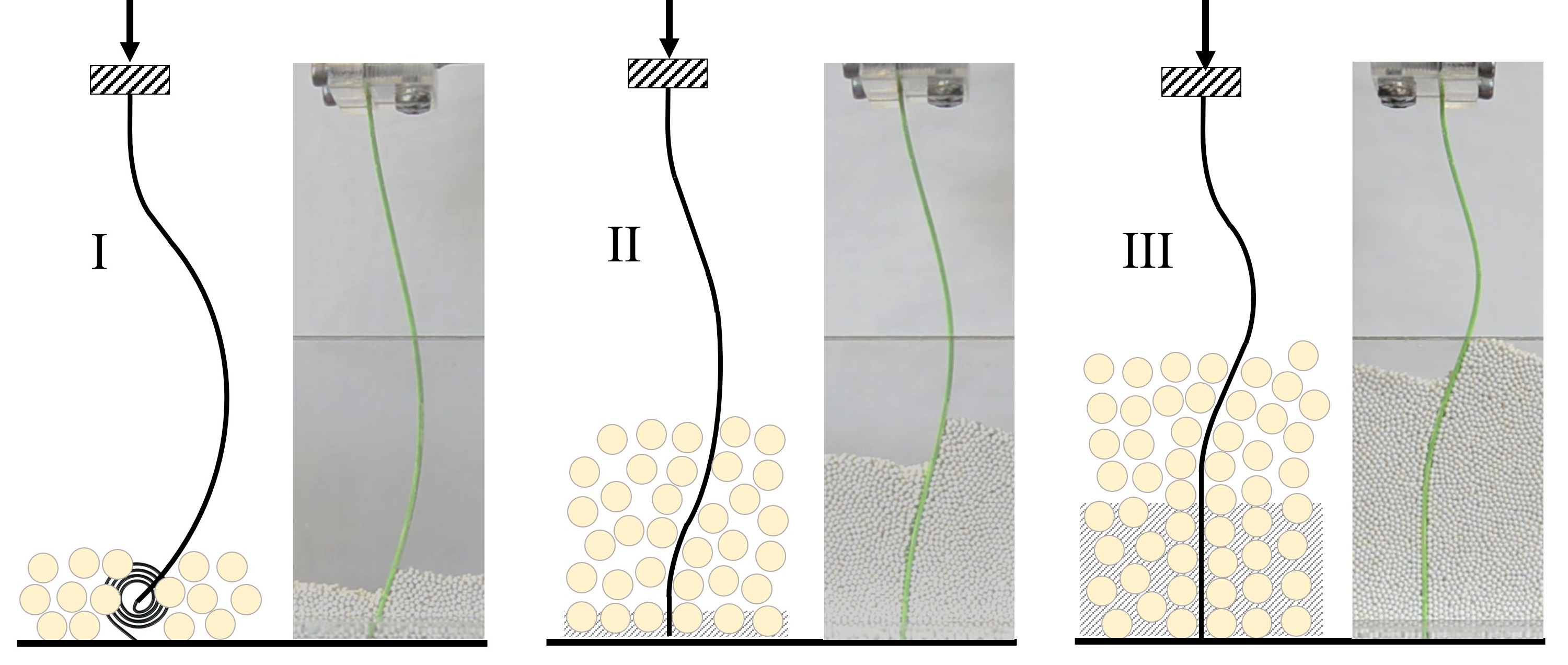
Buckling of elastic beams embedded in granular media
Ahmad R. Mojdehi, Behrouz Tavakol, Wesley Royston, David A. Dillard, Douglas P. Holmes, Extreme Mechanics Letters, 9, 237–244, (2016).
Abstract: In this paper, an experimental and theoretical study of the buckling response of slender elastic beams within granular media is performed. Buckling loads of beams with different flexural rigidity, length, and boundary conditions within granular media of different depths are determined. The Ritz approximate method is implemented to model the buckling response of the beams based on the concept of an overhanging beam on an elastic foundation, using a series of springs whose spring constants change linearly with respect to the depth of the grains. There is good agreement between the experimental results and the theoretical model. There is a characteristic penetration ratio where the beams are not able to sense the boundary condition at the embedded end, resulting in a convergence of the buckling loads. This condition happens when the rigidity of the beam is lower than the effective stiffness of granular support, leading to the confinement of the lower portion of the beam inside the grains, and acting as a secondary boundary condition that is independent of the condition at the end of the beam. We derive a scaling law to characterize this characteristic penetration ratio in terms of a dimensionless stiffness parameter, allowing for the characterization of three distinct interactions between the beam and medium based on the ratio of granular support effective stiffness to the beam’s effective stiffness.
Link: http://www.sciencedirect.com/science/article/pii/S2352431616300335
Paper: Elastocapillary Swelling
Rising Beyond Elastocapillarity
Douglas P. Holmes, P.-T. Brun, Anupam Pandey, and Suzie Protière, Soft Matter, 12, 4886-4890, (2016).
Abstract: We consider the elastocapillary rise between swellable structures using a favorable solvent. We characterize the dynamic deformations and resulting equilibrium configurations for various beams. Our analysis reveals the importance of the spacing between the two beams, and the elastocapillary length, which prescribes the relative magnitude of surface tension and bending stiffness in the system. In particular, we rationalize the transition between coalescence-dominated, bending-dominated, and swelling-dominated regimes, and enumerate the subtle interfacial mechanisms at play in the ratcheting of a fluid droplet trapped between the curling beams.
Link: http://pubs.rsc.org/en/content/articlelanding/2016/sm/c6sm00329j#!divAbstract
Paper: Growing sheets into shells
Geometry and mechanics of thin growing bilayers
Matteo Pezzulla, Gabriel P. Smith, Paola Nardinocchi, and Douglas P. Holmes, Soft Matter, 12, 4435-4442, (2016).
Abstract: We investigate how thin sheets of arbitrary shapes morph under the isotropic in-plane expansion of their top surface, which may represent several stimuli such as nonuniform heating, local swelling and differential growth. Inspired by geometry, an analytical model is presented that rationalizes how the shape of the disk influences morphing, from the initial spherical bending to the final isometric limit. We introduce a new measure of slenderness that describes a sheet in terms of both thickness and plate shape. We find that the mean curvature of the isometric state is three fourths the natural curvature, which we verify by numerics and experiments. We finally investigate the emergence of a preferred direction of bending in the isometric state, guided by numerical analyses. The scalability of our model suggests that it is suitable to describe the morphing of sheets spanning several orders of magnitude.
Link: http://pubs.rsc.org/en/content/articlelanding/2016/sm/c6sm00246c#!divAbstract
arXiv: http://arxiv.org/abs/1509.05259

Paper: Buckling with fluid electrodes
Voltage-induced buckling of dielectric films using fluid electrodes
B. Tavakol and D.P. Holmes, Appl. Phys. Lett., 108, 112901, (2016).
Abstract: Accurate and integrable control of different flows within microfluidic channels is crucial for further development of lab-on-a-chip and fully integrated adaptable structures. Here, we introduce a flexible microactuator that buckles at a high deformation rate and alters the downstream fluid flow. The microactuator consists of a confined, thin, dielectric film that buckles into the microfluidic channel when exposed to voltage supplied through conductive fluid electrodes. We estimate the critical buckling voltage and characterize the buckled shape of the actuator. Finally, we investigate the effects of frequency, flow rate, and pressure differences on the behavior of the buckling structure and the resulting fluid flow. These results demonstrate that the voltage-induced buckling of embedded microstructures using fluid electrodes provides a means for high speed, repeatable attenuation of microfluidic flow.
Link: http://scitation.aip.org/content/aip/journal/apl/108/11/10.1063/1.4944331
arXiv: http://arxiv.org/abs/1601.02866
Video: https://vimeo.com/159996841
Paper: Growing Sheets into Shells in Soft Matter
Our manuscript entitled “Morphing of geometric composites via residual swelling” has been published in the Soft Matter. This work was authored by Matteo Pezzulla, and co-authored by Steven Shillig, Paola Nardinocchi, and Douglas Holmes.
This work was also highlighted on Soft Matter's inside cover:

Understanding and controlling the shape of thin, soft objects has been the focus of significant research efforts among physicists, biologists, and engineers in the last decade. These studies aim to utilize advanced materials in novel, adaptive ways such as fabricating smart actuators or mimicking living tissues. Here, we present the controlled growth-like morphing of 2D sheets into 3D shapes by preparing geometric composite structures that deform by residual swelling. The morphing of these geometric composites is dictated by both swelling and geometry, with diffusion controlling the swelling-induced actuation, and geometric confinement dictating the structure’s deformed shape. Building on a simple mechanical analog, we present an analytical model that quantitatively describes how the Gaussian and mean curvatures of a thin disk are affected by the interplay among geometry, mechanics, and swelling. This model is in excellent agreement with our experiments and numerics. We show that the dynamics of residual swelling is dictated by a competition between two characteristic diffusive length scales governed by geometry. Our results provide the first 2D analog of Timoshenko’s classical formula for the thermal bending of bimetallic beams – our generalization explains how the Gaussian curvature of a 2D geometric composite is affected by geometry and elasticity. The understanding conferred by these results suggests that the controlled shaping of geometric composites may provide a simple complement to traditional manufacturing techniques.
Our latest paper on growing sheets into shells was published in @softmatter (http://t.co/IxekMNma84). Made the inside cover too! #NSFfunded
— Douglas Holmes (@dpholmes) July 17, 2015


