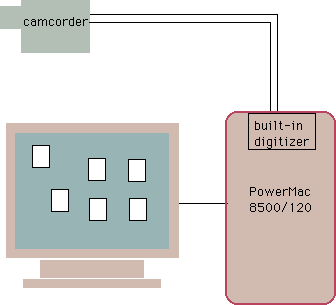
Figure 1. Schematic of the collision detection demo set-up
The NTSC signal from the camcorder is digitized by the built-in digitizer. The digitizer action is controlled from Collision Demo, a modified version of the public-domain program NIH Image. Collision Demo works at about 3 frame s per second on the PowerMac 8500/120, and provides warning about impending collisions. The general outline of the collision warning method is as follows:
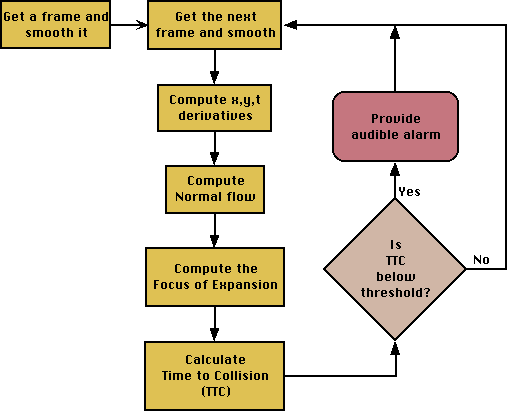
Figure 2. Flow chart of the collision
warning method We explain each of the steps in detail below:
Computation of derivatives
Figure 3. x and y derivative
kernels Results of applying this kernel on an image are shown in the figure
below. The image, its x-derivative and y-derivative are shown, respectively
from left to right.
The temporal derivative is computed as the pixel-wise difference between
the two smoothed frames.
Flow computation
Near-flat intensity distribution and noisy spots give rise to large
normal flow magnitude, and rounding approximations give rise to small flow
measurements where none exitst. Thus, normal flow measurements with very
low or large magnitude are ignored.
If the size of the moving region is larger than a threshold, the 3D
motion is considered to be self-motion; otherwise, the moving object is
isolated and all further processing is restricted to the moving object
(the moving object is enclosed by a white re ctangle in the display window).
FOE Computation
Computation of Time to Collision (TTC)
The parameters a2 and
a6
encode the divergence of the flow. It can be shown that for surfaces
that give rise to a flow that is nearly affine, the TTC is giv en by the
expression where xh and yv are
transformed coordinates with the FOE as the origin. The TTC can now be
computed.
Figure 5. Sample result sequences
demostrating collision warning
Figure 6. A typical indoor image,
and edge distribution of a sequence containing this image Contrary to our assumption (but consistent with empirical observations
in the literature on statistics of indoor images), we found a skewed distribution,
with peaks corresponding to the horizontal and vertical edges. However,
an analysis of the effect of this skewed distribution suggests that a preponderance
of vertical and horizontal edges will not affect-and in fact enhance-the
performance of our FOE detection algorithm, provided that the 3-D horizontal
and vertical edges are projected as horizontal and vertical edges on the
image plane (not necessarily in that order-for e.g., a vertical edge could
project as a horizontal edge on the image by rotating the camera by 90
degrees). This is due to the fact that we use the horizontal and vertical
axes as our reference frames to project the components of the normal flow
(see the explanation for vertical edges in the
appendix).
The preceding observations do not imply, however, that the method will
fail when the distribution of edges is skewed in an unfavorable fashion.
In order to perform a complete analysis of failure, we should consider
not only the edge distribution, but also the motion direction distribution.
Since this joint distribution is not well-studie d, we will not conduct
the extended analysis. We conclude by noting that in all real, indoor sequences
that we processed, the collision warning computation was successful.
Theorem:With high probability (greater than 0.5), the signs
of the components of a normal flow vector agree with the signs of the components
of the corresponding optic flow vector, providing the local intensity gradient
direction is distributed uniformly.
Proof:
For the x component of this (normal) vector to have the same sign as
the x component of the optic flow vector,
cos (q-a) cos (a) cos(q) > 0.
We consider two possibilities:
The first situation occurs if |q-a| < p/2, and if a and q are
in the same vertical set of quadrants (first and fourth, or second and
third). For a given q , a has a range of p-q in which an agreement of signs
results. For the second situation, | 2 p + q - a | < p/2, and a and
q must be in in the same horizontal set of quadrants (first and second,
or third and fourth). This corresponds to a range of p-q for a. Since the
total possible range for a is 0 to 2 p, assuming a uniform distribution
for a,the prob ability that the signs of the x components agree is ( p
- q ) / p.
In passing, we note that for a =0, p (vertical
edges), the signs of the x components always agree!
Using a similar argument, it can be easily shown that the probability
that the y components agree is (p/2+q )/p.
The x,y, and t derivatives are computed from two subsequent frames
in the following way. First, the two frames are smoothed (within the processing
loop, only the current frame is smoothed, the earlier frame has been smoothed
in the previous iteration). Th e smoothed first image is convolved with
x
and y derivative kernels shown below:
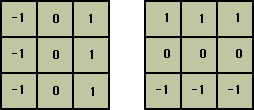

Figure 4. An image, its x-derivative,
and y-derivative
Normal flow is computed at locations where the local spatial gradient
magnitude is above a threshold value. The gradient method based on the
optic flow constraint equation shown below is used to calculate the normal
flow:
![]()
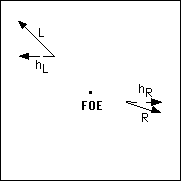
The focus of expansion (FOE) is computed based on the principle that
flow vectors are oriented in specific directions relative to the FOE. The
horizontal component hLof an optic
flow vector Lto the left of the FOE points
leftward. For an optic flow vector R to the
right of the FOE, the horizontal component hR
points rightward, as shown in the figure on the left. By a c ounting method,
we can determine the location about which a majority of horizontal components
diverge. We have extended this principle to the field of normal flow vectors.
Thus, we can find the FOE from a normal flow vector field, providing that
the inten sity gradient (edge) distribution in the image is uniform (i.e.,
the probability that a certain orientation is seen in an image location
is the same as for any other orientation). The proof for this method is
given in the Appendix .
The time to collision (TTC) can be computed from the parameters of
the first-order approximation to the optic flow field. The first-order
(affine) approximation is given by
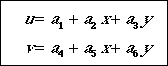
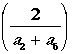 .
The parameters a2 and a6
can be computed from the normal flow over a 2-D regio n. However, to speed
up the computation, we consider only the horizontal line and the vertical
line passing through the FOE. The following figure illustrates the simplification
achieved by this choice:
.
The parameters a2 and a6
can be computed from the normal flow over a 2-D regio n. However, to speed
up the computation, we consider only the horizontal line and the vertical
line passing through the FOE. The following figure illustrates the simplification
achieved by this choice:
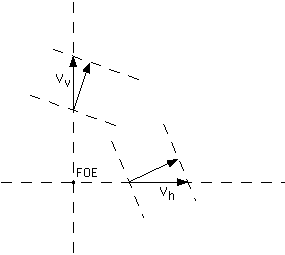
Arbitrary local edge directions have been chosen to show the normal
flow of two optic flow vectors-one along the vertical line and the other
along the horizontal line passing through the FOE. Note that these optic
flow vectors must lie along these li nes because of the structure of translational
flow fields. It can be easily shown that the magnitude of the horizontal
optic flow vector is
![]() and that of the vertical opti c flow vector is
and that of the vertical opti c flow vector is ![]() ,
where E is the spatio-temporal intensity function. These
derivatives have been computed earlier. From several
measu rements along the horizontal and vertical lines, we can calculate
the desired affine parameters as follows:
,
where E is the spatio-temporal intensity function. These
derivatives have been computed earlier. From several
measu rements along the horizontal and vertical lines, we can calculate
the desired affine parameters as follows:
![]() ,
,
Shown below are results from some image sequences.
If object motion is sensed, a white rectangle is drawn around the object.
The FOE is shown as a small white square. No temporal integration is performed
(all results are based on 2-frame processing). The first two sequences
(the pretzel box sequence and the coffee
cup sequence were shot off-line and then processed; the lab
walk sequence was processed on-line). All the imag e sequences were
a fourth of normal NTSC size: 120 X 160 pixels. The speed of the animation
is not related to the speed of processing (various factors come in to play,
including the speed of the machine on which the browser is running). We
estimated empir ically that our implementation in NIH Image v1.60 running
on a PowerMac 8500/120/32M runs at 3 frames/sec. We believe that a hardware
implementation will run in real-time.



Discussion
Advantages of this method
There are several advantages to our approach. We list them below:
Edge Distribution
Even if the FOE computation seemed to work well, we wanted to ascertain
that the edge distribution in the images was as assumed (uniform: see the
appendix).
We modified the FOE computation program to calculate the edge distributio
n in indoor images (sequences). The advantage of modifying the FOE program
(instead of writing a new one) was that the statistics considered only
edges of the same type (satisfying the same gradient and velocity thresholds)
as in the FOE computation. Res ults from a typical indoor scene are shown
below: first a sample image from the sequence, second the distribution
of the edge orientations (0 degrees corresponds to horizontal, 90 degrees
is vertical).

Appendix A
(also see: empirical analysis of edge distribution
in real images)
Let the local gradient subtend an angle a, and the optic flow vector
subtend an angle q, with the x axis. Without loss of generality, we can
assume that both a and q are in the range 0 to p/2 (p*d is the circumference
of a circle with diameter d). The loc al gradient is along [cos(a), sin(a)]
and the optic flow vector is along [cos(q), sin(q)]. The normal flow vector
is in the direction cos (q-a)[cos(a), sin(a)].
2. cos(q-a) < 0 and cos (a) cos (q) < 0.
This report was prepared by Dr. Lucia
M. Vaina. November 26, 1996.